Jednonogi robot - czyli nauka wstawania
Olgierd Humeńczuk
Sprawozdanie z dużego zadania ze sztucznej inteligencji sem. 2006/2007.
Wrocław 22.06.07
1. Opis zadania
Problem, którym postanowiłem się zająć w ramach dużego projektu ze sztucznej inteligencji, polega na nauczeniu robota jak przenieść się z pozycji horyzontalnej do wertykalnej
i ją zachować. Robot posiada tylko jedną nogę zbudowaną z dwóch ramion połączonych zawiasem, z których jedno z nich służy za przeciwwagę pomocną w utrzymywaniu równowagi.
Maszyna jest przytwierdzona na stałe do podłogi za pomocą kolejnego zawiasu. Maszyna może poruszać się tylko w dwóch współrzędnych x i y. Jedyną częścią którą robot może
sterować jest górne ramie, które poruszane jest za pomocą silniczka.
2. Metoda
Do rozwiązania problemu użyłem metody uczenia ze wzmocnieniem ( ang. reinforcement learning ). Jest to jedna z metod pozwalająca na uczenie bez nadzoru korzystająca jedynie z
prostej oceny wykonanych akcji ( kary lub nagrody ). Pozwala ona na wyuczenie maszyny złożonych czynności, które metodą prób i błędów są przez nią doskonalone. Aby tego
dokonać
metoda uczenia ze wzmocnieniem wymaga podania przestrzeni stanów i akcji, oraz ustalenia za co będzie otrzymywać nagrody. Reszta, czyli znalezienie optymalnej kolejności
wykonywanych akcji w
zależności od stanu, w którym znajduje się maszyna, odbywa się automatycznie. Algorytmów znajdujących to optymalne rozwiązanie, zwane tak polityką, jest dużo. Ja użyłem na
początku jednego z najprostszych:
Q-learning. Algorytm Q-learning wziął swą nazwę z przyjętej terminologii. Literą Q bowiem, oznacza się zbiór wartości określających
korzyści wykonania akcji a(t) w dowolnym stanie x(t). Q-learning polega na ciągłej aktualizacji tego zbioru tuż po wykonaniu akcji. Nagroda lub kara przyznawana jest w
zależności czy wykonana akcja przyniosła w porównaniu z poprzednią korzyść czy pogorszyła sytuację maszyny. Oto schemat omówionego algorytmu:
Niestety z pewnych względów, omówionych w podrozdziale 5 i 6 tego sprawozdania, algorytm Q-learning nie dał zadowalających wyników. Postanowiłem zaimplementować
inny algorytm: AHC ( z ang. Adaptive Heuristic Critic ). Algorytm ten różni się tym od algorytmu Q-learning tym, że w celu aktualizacji wartości akcji dla stanów posługuje się
wartościami stanów, a nie tak jak w przypadku Q-learning samymi wartościami akcji. Oto schemat AHC:
Parametrami algorytmu Q-learning są: beta i gamma, odpowiednio gamma odpowiada za stopień w jakim algorytm ma wykorzystywać to czego się już nauczył, natomiast
beta odpowiada za szybkość uczenia. Dodatkowym parametrem AHC jest alpha, który oznacza to samo co beta tylko stosowany jest dla szybkość wartościowania stanów.
2.1. Strategia wyboru akcji
Kolejną rzeczą o jaką należy się zatroszczyć implementując wymienione alg. jest sposób wyboru akcji. W materiałach znajdujących się na końcu tego sprawozdania
znajduje się omówienie kilku z nich. W swoim eksperymencie użyłem tylko jednej z nich, która okazała się wystarczająca. Jest to strategia epsilon-zachłanna.
Polega ona na częściowo losowym wyborze akcji. Strategia przyjmuje jako parametr wartość epsilon, która określa jak bardzo losowy będzie to wybór. Następnie
losowana jest wartość i jeśli ta wartość jest mniejsza od epsilon to wybór ograniczony jest do akcji o maksymalnej wartości przydatności w danym stanie, w przeciwnym
wypadku wybierana jest losowa akcja. Dobór parametru epsilon jest bardzo ważny ponieważ ustala on granicę między eksploracją a eksploatacją. W dalszej części kwestia ta
będzie jeszcze przeze mnie omawiana.
2.2. Reprezentacja stanów
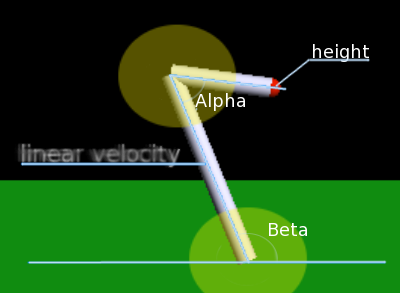
Do uruchomienia algorytmu uczenia pozostaje tylko zastanowienie się nad tym jaka ma być reprezentowane środowisko - czyli ilu stanów użyć i czym one powinny być.
W moim programie użyłem następującej reprezentacji:
- alpha - kąt między ramionami robota
- beta - kąt między "nogą" robota a ziemią
- linear velocity - prędkość liniowa "nogi"
- height - wysokość na jakiej znajduje się czerwona kula umieszczona na końcu ruchomego ramienia
W eksperymentach używałem jako nagrody najpierw wysokości ( height ) potem eksperymentowałem z wartością kąta alpha. Problemem w reprezentacji stanów jest jak
modelować za pomocą dyskretnych stanów ciągłe środowisko tak jak w przypadku rozwiązywanego przeze mnie problemu. Rozwiązań jest kilka, ja użyłem po prostu
przedziałowej reprezentacji wartości. Jest to oczywiście problem ponieważ dokładność zależy od ilości stanów. U mnie liczba stanów z 2048 początkowych
została zwiększona do 131 072. Spowodowało to wzrost dokładności kosztem zużycia pamięci i czasu uczenia.
3. Co w kodzie piszczy?
Zadanie zaimplementowałem w języku C++ używając silnika fizycznego ODE ( Open Dynamics Engine ). Do wizualizacji wykorzystałem bibliotekę OpenGL. Program wykorzystuje również
biblioteki GTK+, GTK+mm, GTK+extGLmm. Działa pod systemami z rodziny Linux. Implementacja algorytmu uczenia opiera się na dwuwymiarowej tablicy wartości poszczególnych akcji,
wartości stanów, oraz kilku metodach pomocniczych, które np. obliczają potrzebne wartości w tym numer stanu do którego trafił robot po wykonaniu akcji. Wszelkie obliczenia
fizyczne wykonywane są przez silnik ODE. Klasa zawierająca implementację algorytmów i strategii, jest zupełnie odrębną klasą i jest wykorzystywana jako czarna skrzynka. Oto
schemat przepływu informacji w głównej pętli mojego programu:
Przepływ informacji w programie:
- Wyświetl obiekty
- Przelicz położenie obiektów w następnym kroku wykorzystując ODE
- Podaj informacje o obiektach obiektowi odpowiedzialnemu za uczenie
- Przelicz wartości akcji i stanów ( tylko w przypadku alg. AHC )
- Wykonaj akcję jaką zwrócił obiekt odpowiedzialny za uczenie
- Przejdź to punktu 1.
4. Przykład działania programu
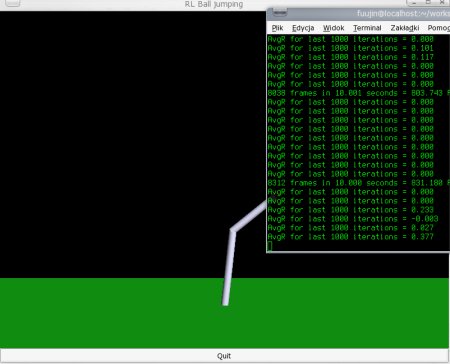
To jest przykładowy zrzut ekranu podczas
działania mojego programu. W centralnej części znajduje się "podgląd" na robota, który stara się wykonać zadanie, dodatkowo w konsoli użytkownik otrzymuje dane na temat
postępów w uczeniu. Co 100000 iteracji wypisywana jest średnia nagroda, jaka została przyznana przez algorytm. Dostępna jest opcja przyspieszenia uczenia o 100 000, 3 00 0000
oraz 19 000 000 iteracji z pominięciem wyświetlania.
5. Wyniki
Pierwsze próby uczenia algorytmem Q-learning były bardzo nieudane. Spowodowane było to złym ustawieniem stałych fizycznych takich jak masy, maksymalne prędkości, długości
ramion oraz zbyt małą ilością stanów i złym doborem stałych algorytmu. Wraz z większą ilością wykonanych eksperymentów poprawiałem na bieżąco ustawienia wyżej wymienionych
wartości. Największy problem miałem z ustawieniami fizyki, ważnym elementem świata okazały się być opory, których odpowiednie dostosowanie zaowocowało poprawą wyników uczenia.
Równie ważnym, jeśli nie najważniejszym parametrem algorytmu, okazał się epsilon czyli parametr określający równowagę między eksploatacją i eksploracją. Przy jej zachwianiu
nie można oczekiwać dobrych wyników. Zbyt duże ustawienie wartości eksploatacji w znacznej mierze hamuje proces uczenia, czasem wręcz zatrzymując go i powodując, że algorytm
utyka w lokalnych maksimach, natomiast zbyt mała wartość tego parametru zaowocuje szalonym robotem, który będzie co prawda badał dogłębnie przestrzeń rozwiązania, ale nie
będzie korzystał z tego czego się przy okazji nauczył. Po dużej ilości wykonanych eksperymentów zachowanie się mojego robota nie było jednak zachwycające. Nauczył się
co prawda jak odbić się od podłogi w taki sposób, żeby osiągnąć kąt 90 stopni między podłożem a "nogą" jednak prędkości jakie osiągał były zbyt szybkie i najczęściej
lądował w pozycji symetrycznej do tej z której startował. Kolejnym problemem jaki się pojawił był mały czas jaki robot spędzał w okolicy pozycji jaką powinien utrzymywać i tym
samym mała ilość eksploracji odpowiadających tej pozycji stanów. Po kilkunastu milionach iteracji robot cały czas nie był nawet bliski utrzymania równowagi w pionie.
Postanowiłem sprawdzić jak będzie sobie radził robot po nauce algorytmem AHC, oraz jaki będzie miała wpływ na naukę zmiana funkcji nagrody z wysokości na kąt między "nogą", a
podłożem. AHC zgodnie z moimi oczekiwaniami poradził sobie z postawionym problemem lepiej niż Q-learning. Po pierwsze dlatego, że w alg. AHC wartościowane są stany i na ich
podstawie wartości akcji dla poszczególnych stanów. Mój problem postawienia robota w pionie jest problemem w którym ważniejsze jest osiągnięcia odpowiedniego stanu niż
wykonanie konkretnych akcji, więc algorytm AHC lepiej sobie z nim poradził. Po drugie zmieniłem funkcję nagrody na wartość kąta, największa nagroda przypada kątowi 90 stopni,
natomiast największa kara kątom 0 i 180 stopni. Algorytm AHC testowałem dla obu funkcji nagród i dla obu z nich średnio po 19 000 000 iteracji robot osiągał pozycję pionową,
jednak różnymi sposobami. Dla nagród opartych na wartości wysokości robot starał się mieć wyciągniętą górną kończynę w pionie i delikatnie nią manipulować, natomiast dla
nagród opartych na kącie, ramię pozostawało zgięte i robot starał się odbić w taki sposób aby zatrzymać się w pionie używając ramienia jako przeciwwagi, która wyhamuje zbyt
dużą prędkość. Po wprowadzonych zmianach zadowolony jestem z wyników, robot co prawda nie na długo zatrzymuje się w okolicach pożądanej pozycji, ale bardzo szybko do niej
powraca i widać, że nauka przynosi zmiany. Wydaje mi się jednak, że można uzyskać trochę lepsze wyniki dobierając dokładniej współczynniki algorytmu i być może zmieniając
wartości stanów oraz ustawienia fizyki.
6. Wnioski
Podczas pracy nad omawianym projektem, nie mogłem oprzeć się wrażeniu, że wybrany przeze mnie projekt, na początku wydawał się być znacznie prostszym. Podobne pomysły
zostały z powodzeniem zrealizowane, czego dowody można znaleźć na stronach poświęconych wykorzystywaniu uczenia ze wzmocnieniem w robotyce i automatyce. Moje wyniki nie są
oszałamiające i mam świadomość tego, że można nad tym projektem jeszcze dużo popracować, aby poprawić jego zdolność uczenia. Istnieje kilka algorytmów, które nadawałyby się
lepiej do tego celu niż Q-learning czy AHC. Przy rozwiązywaniu tego i podobnych problemów, gdzie środowisko jest ciągłe i jego dyskretyzacja powoduje drastyczny wzrost liczby
stanów ( proszę sobie wyobrazić ilość stanów gdyby ten sam problem za modelować używając trzech wymiarów zamiast dwóch ), powinno się używać reprezentacji funkcji poprzez ich
aproksymację lub dynamiczne zwiększanie ilości stanów tam gdzie to jest potrzebne. Jednym z ciekawszych sposobów
na poradzenie sobie z ciągłym środowiskiem jest użycie sieci neuronowych jako decydentów, czyli tego elementu który decyduje o tym jaką akcję na podstawie informacji o świecie
powinna podjąć maszyna. Metoda uczenia ze wzmocnieniem stosowana jest w robotyce i służy między innymi do programowania sterowników robotów. Nauka chodzenia, czy pilotażu
śmigłowca, gry w pokera czy tetrisa to problemy idealne dla tej metody. Uczenie ze wzmocnieniem jest bardzo prostą ideą, która może być dowolnie usprawniania i jest bardzo
dynamicznie rozwijana. Podsumowując jest to obliczeniowe podejście do uczenia się celowego zachowania na podstawie interakcji ze środowiskiem, gdzie źródłem informacji
trenującej, która ma charakter wartościujący jakość działania maszyny, jest ocena skuteczności podejmowanych akcji.
7. Materiały

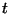 :
:
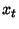 ;
;
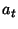 do wykonania w stanie
do wykonania w stanie
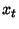 ;
;
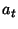 ;
;
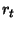 i następny stan
i następny stan 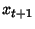 ;
;
 ;
;
 .
.
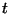 :
:
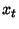 ;
;
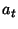 do wykonania w stanie
do wykonania w stanie 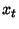 na podstawie
na podstawie
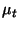 ;
;
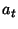 ;
;
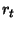 i następny stan
i następny stan 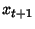 ;
;
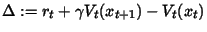 ;
;
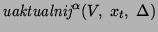 ;
;
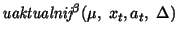 ;
;
 Do uruchomienia algorytmu uczenia pozostaje tylko zastanowienie się nad tym jaka ma być reprezentowane środowisko - czyli ilu stanów użyć i czym one powinny być.
W moim programie użyłem następującej reprezentacji:
Do uruchomienia algorytmu uczenia pozostaje tylko zastanowienie się nad tym jaka ma być reprezentowane środowisko - czyli ilu stanów użyć i czym one powinny być.
W moim programie użyłem następującej reprezentacji:
 To jest przykładowy zrzut ekranu podczas
działania mojego programu. W centralnej części znajduje się "podgląd" na robota, który stara się wykonać zadanie, dodatkowo w konsoli użytkownik otrzymuje dane na temat
postępów w uczeniu. Co 100000 iteracji wypisywana jest średnia nagroda, jaka została przyznana przez algorytm. Dostępna jest opcja przyspieszenia uczenia o 100 000, 3 00 0000
oraz 19 000 000 iteracji z pominięciem wyświetlania.
To jest przykładowy zrzut ekranu podczas
działania mojego programu. W centralnej części znajduje się "podgląd" na robota, który stara się wykonać zadanie, dodatkowo w konsoli użytkownik otrzymuje dane na temat
postępów w uczeniu. Co 100000 iteracji wypisywana jest średnia nagroda, jaka została przyznana przez algorytm. Dostępna jest opcja przyspieszenia uczenia o 100 000, 3 00 0000
oraz 19 000 000 iteracji z pominięciem wyświetlania.