Metody i Algorytmy Sztucznej Inteligencji
Raport
prezentuje problem poszukiwania najlepszego rozmieszczenia
maszyn w hali produkcyjnej, minimalizującego całkowite koszty
transportu
elementów w hali produkcyjnej. Znalezienie optymalnego rozwiązania jest
trudne
ponieważ jest to problem NP-trudny. Rozwiązanie problemu otrzymujemy
wykorzystując algorytmy konstrukcyjne oraz algorytm poszukiwań z
zabronieniami Tabu
Serach wspomagany metodą skoku
powrotnego (MSP). W raporcie przedstawiono wyniki badań komputerowych,
które
ukazują rezultaty otrzymanych rozwiązań oraz jaki wpływ na otrzymane
wyniki ma
zastosowanie algorytmu Tabu
Serach do powyższego problemu.
Problem wielorzędowego rozmieszczenia maszyn w hali polega na takim rozmieszczeniu maszyn, które minimalizuje całkowite koszty transportu półproduktów (np. detali) pomiędzy maszynami. Wyliczany koszt transportu zależy w tym przypadku przede wszystkim od:
· odległości między maszynami
· oraz jednostkowego kosztu transportu
Poniżej
przedstawiono, jedną z możliwych, koncepcję rozwiązania problemu, w
oparciu o
kombinatoryczny model wielorzędowego rozmieszczenia maszyn (stanowisk
roboczych) w hali produkcyjnej, który określa specyficzny sposób
rozmieszczenia
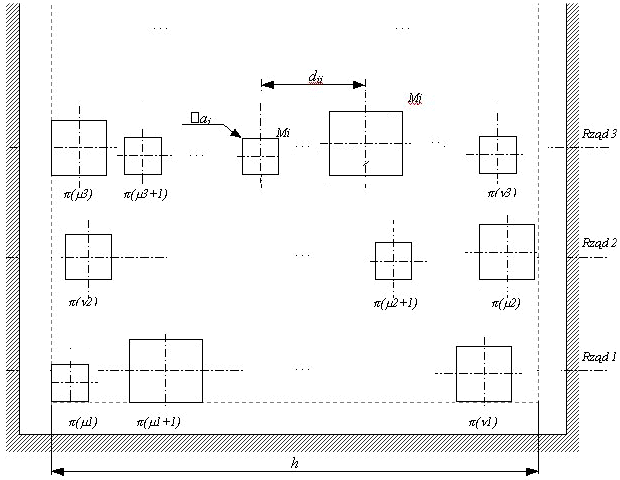
maszyn zgodny z rysunkiem nr 1. Dla rozwiązania
problemu zaproponowano
algorytmy konstrukcyjne, których wynik został poprawiony przez
metaheurystykę
tabu, tj. algorytm TS (ang. Tabu Search).

Rys.
1. Wielorzędowe rozmieszczenie maszyn w hali produkcyjnej.
3. Opis
modelu matematycznego problemu
Niech 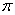 będzie permutacją
numerów
będzie permutacją
numerów 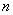 maszyn (stanowisk
roboczych) które podlegać będą rozmieszczeniu. Dalej, niech
maszyn (stanowisk
roboczych) które podlegać będą rozmieszczeniu. Dalej, niech 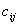 będzie kosztem
jednostkowym (jednostki półproduktu na jednostkę odległości) transportu
półproduktów
pomiędzy maszynami
będzie kosztem
jednostkowym (jednostki półproduktu na jednostkę odległości) transportu
półproduktów
pomiędzy maszynami 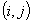 oraz
oraz 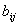 jest
odległością transportu jednej jednostki półproduktu pomiędzy tymi
maszynami,
gdzie tablica odległości
jest
odległością transportu jednej jednostki półproduktu pomiędzy tymi
maszynami,
gdzie tablica odległości 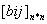 jest
wyliczana dla każdej permutacji maszyn
jest
wyliczana dla każdej permutacji maszyn 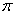 i zależy zarówno od
położenia maszyn określonych przez permutację
i zależy zarówno od
położenia maszyn określonych przez permutację 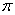 oraz od zastosowanego
systemu transportu międzymaszynowego w hali. Przy tak przyjętych
założeniach
możemy formalnie zapisać całkowity koszt transportu półproduktów
pomiędzy
maszynami hali w postaci następującej funkcji celu:
oraz od zastosowanego
systemu transportu międzymaszynowego w hali. Przy tak przyjętych
założeniach
możemy formalnie zapisać całkowity koszt transportu półproduktów
pomiędzy
maszynami hali w postaci następującej funkcji celu:
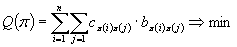
gdzie: 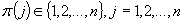
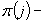 numer
maszyny usytuowanej na
numer
maszyny usytuowanej na 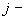 tej
pozycji w hali maszyn.
tej
pozycji w hali maszyn.
Permutacja  wyznacza kolejność z
jaką będą rozmieszczane maszyny w hali; sposób rozmieszczenia ilustruje
rysunek
nr 1. Niech
wyznacza kolejność z
jaką będą rozmieszczane maszyny w hali; sposób rozmieszczenia ilustruje
rysunek
nr 1. Niech 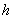 jest maksymalną
długością rzędów w hali produkcyjnej,
jest maksymalną
długością rzędów w hali produkcyjnej, 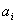 jest szerokością
maszyny i oraz
jest szerokością
maszyny i oraz 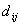 minimalnym
odstępem między maszynami
minimalnym
odstępem między maszynami 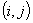 . Minimalna długość
rzędu potrzebna do rozmieszczenia wszystkich maszyn zgodnie z
permutacją
. Minimalna długość
rzędu potrzebna do rozmieszczenia wszystkich maszyn zgodnie z
permutacją 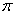 jest równa:
jest równa:
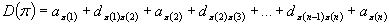
W przypadku
gdy minimalna długość rzędu wszystkich maszyn 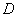 przewyższa maksymalną
długość rzędu hali
przewyższa maksymalną
długość rzędu hali 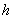 ,
,
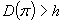 ,
tworzymy dodatkowe rzędy w których kolejno
rozmieszczamy maszyny zgodnie z permutacją
,
tworzymy dodatkowe rzędy w których kolejno
rozmieszczamy maszyny zgodnie z permutacją 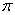 .
Niech
.
Niech 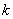 jest numerem
porządkowym rzędu maszyn w hali. Każdy rząd
jest numerem
porządkowym rzędu maszyn w hali. Każdy rząd 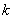 hali jest utworzony z
maszyn podsekwencji
hali jest utworzony z
maszyn podsekwencji 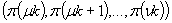 permutacji
permutacji 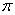 .
Długość rzędu
.
Długość rzędu 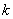 maszyn określona jest
zależnością:
maszyn określona jest
zależnością:
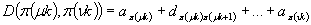
gdzie 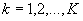
 - jest liczbą
utworzonych rzędów maszyn.
- jest liczbą
utworzonych rzędów maszyn.
Do
pierwszego rzędu maszyn należą maszyny podsekwencji 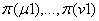 spełniające warunki:
spełniające warunki:
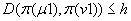

Sekwencja maszyn umieszczona w drugim rzędzie spełnia zależności:
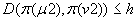
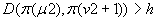
I tak dalej, gdzie:
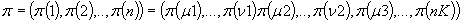
i 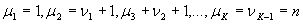
Aby rozwiązać tak zdefiniowany problem, wykorzystamy dwa algorytmy konstrukcyjne, których celem jest pozyskanie dobrego rozwiązania początkowego (wstępnego rozmieszczenia maszyn), które będzie rozwiązaniem bazowym dla algorytmu Tabu Serach.
Algorytm "Konstrukcyjny
1" (o złożoność 0(n2)), na podstawie
jednostkowego
kosztu transportu materiałów 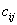 rozmieszcza maszyny
tak aby zminimalizować "lokalne" koszty transportu.
rozmieszcza maszyny
tak aby zminimalizować "lokalne" koszty transportu.
Schemat algorytmu "Konstrukcyjnego 1"
Krok 1.
W macierzy 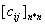 znajdź
maksymalny element
znajdź
maksymalny element
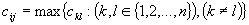
i przypisz 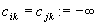 dla
dla 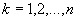 oraz jako rozwiązanie
częściowe przypisz
oraz jako rozwiązanie
częściowe przypisz
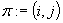 .
.
Krok 2.
Jeżeli częściowe rozwiązanie 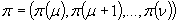 nie zawiera wszystkich
maszyn to dla macierzy kosztów
nie zawiera wszystkich
maszyn to dla macierzy kosztów 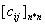 znajdź
maksymalny element:
znajdź
maksymalny element:
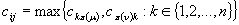
Jeżeli 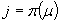 to przypisz
to przypisz 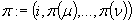 oraz
oraz 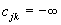 dla
dla 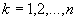 ;
w przeciwnym wypadku podstaw
;
w przeciwnym wypadku podstaw 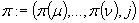 oraz
oraz
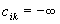 dla
dla
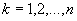 .
.
Algorytm "Konstrukcyjny 2" (o złożoności 0(nlogn)), wyznacza sekwencję maszyn według obliczonej funkcji priorytetu:
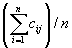
rozmieszczając
maszyny
rozpoczynając od największej wartości priorytetu - w położeniu
centralnym
sekwencji 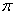 ,
do najmniejszej wartości priorytetu - położenia skrajne
sekwencji
,
do najmniejszej wartości priorytetu - położenia skrajne
sekwencji 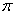 .
.
Schemat algorytmu "Konstrukcyjnego 2":
Krok 1.
Dla
każdej maszyny 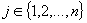 oblicz wartość
priorytetu:
oblicz wartość
priorytetu:
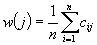
Krok 2.
Utwórz
listę
maszyn 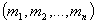 według niemalejącej
wartości funkcji priorytetu:
według niemalejącej
wartości funkcji priorytetu:

Krok 3.
Wyznacz rozwiązanie 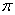 przypisując
przypisując
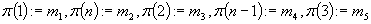 ,
i tak dalej.
,
i tak dalej.
Otrzymane w wyniku zastosowania algorytmów konstrukcyjnych rozwiązanie, poprawiamy przez zastosowanie algorytmu Tabu Search. Do otrzymania lepszego rozwiązania stosujemy algorytm TS wyposażony w mechanizmy dywersyfikujące i intensyfikujące proces poszukiwań takie jak: pamięć krótko terminowa, pamięć długo terminowa, metoda skoku powrotnego.
Oznaczenia:
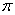 - Rozwiązanie należące
do zbioru rozwiązań dopuszczalnych.
- Rozwiązanie należące
do zbioru rozwiązań dopuszczalnych.
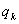 - Wartość funkcji
celu w
- Wartość funkcji
celu w 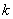 -
tej iteracji.
-
tej iteracji.
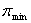 -
Rozwiązanie poprawione przez algorytm TS.
-
Rozwiązanie poprawione przez algorytm TS.
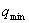 -
Najlepsza wartość funkcji celu znaleziona przez algorytm
TS.
-
Najlepsza wartość funkcji celu znaleziona przez algorytm
TS.
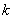 -
Licznik wykonanych iteracji.
-
Licznik wykonanych iteracji.
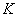 - Globalna liczba
iteracji przewidzianych do wykonania.
- Globalna liczba
iteracji przewidzianych do wykonania.
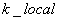 - Licznik iteracji
wykonanych bez poprawy funkcji celu.
- Licznik iteracji
wykonanych bez poprawy funkcji celu.
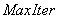 - Liczba iteracji
wykonana bez poprawy funkcji celu po której następuje zakończenie pracy
algorytmu.
- Liczba iteracji
wykonana bez poprawy funkcji celu po której następuje zakończenie pracy
algorytmu.
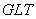 - Górna lista tabu –
pamięć krótkoterminowa.
- Górna lista tabu –
pamięć krótkoterminowa.
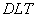 - Dolna lista tabu –
pamięć długoterminowa.
- Dolna lista tabu –
pamięć długoterminowa.
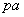 - Poziom aspiracji.
- Poziom aspiracji.
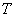 -
Okres tabu.
-
Okres tabu.
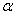 - Stała różnicowania
procesu poszukiwań.
- Stała różnicowania
procesu poszukiwań.
Schemat algorytmu Tabu Search z zastosowaniem pamięci krótkoterminowej, długoterminowej i kryterium aspiracji:
Krok 1.
Początek poszukiwania podstaw:
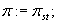
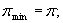
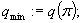
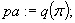
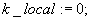
Krok 2.
Dla
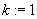 do
do 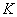 wykonaj
wykonaj
a)
Wyznacz najlepsze rozwiązanie w otoczeniu:
Jeżeli 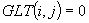 to
to
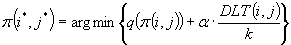
Jeżeli 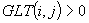 to
to
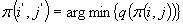
Podstaw:
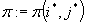
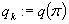
b) Poprawa rozwiązań:
Jeżeli 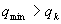 to podstaw:
to podstaw:
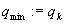
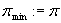
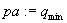
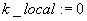
Jeżeli 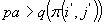 to wykonaj
instrukcje:
to wykonaj
instrukcje:
Podstaw:
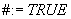
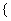
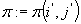
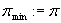
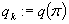
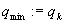
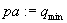
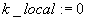
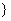
Podstaw
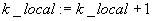
Jeżeli 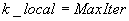 to STOP;
to STOP;
c) Korekta stanu pamięci:
Dla  podstaw
podstaw 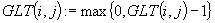 .
.
Jeżeli
wykonano instrukcje 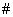 to podstaw:
to podstaw:
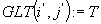 i
i 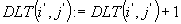
w przeciwnym wypadku:
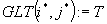 i
i 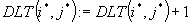
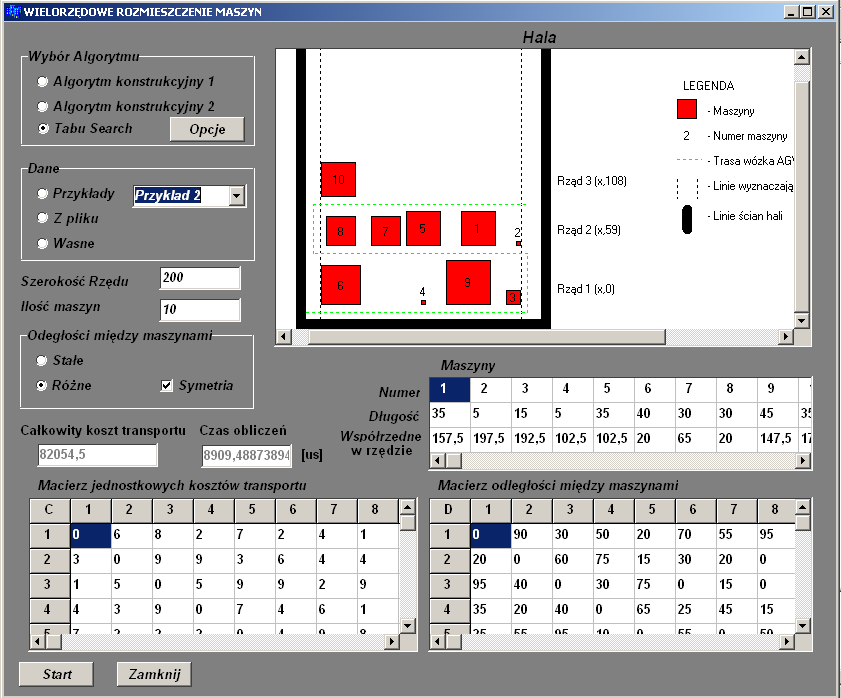
Rys. 2. Widok interfejsu graficznego programu użytego do obliczeń
W ramach projektu został wykorzystany program, którego interfejs graficzny został pokazany na rysunku nr 2. Program został napisany przez projektanta w języku C++ i uruchamiany jest w systemie Microsoft Windows. W programie zostały zaimplementowane omówione powyżej algorytmy.
Po uruchomieniu programu należy wybrać źródło danych. Do testów zostały stworzone gotowe zestawy danych dla 5, 10, 15, 20 liczby maszyn. Można z nich skorzystać zaznaczając w panelu Dane opcje Przykłady a następnie wybrać jeden z nich. Dodatkowo możemy wprowadzać zmiany dla wybranych danych m. in. możemy modyfikować poszczególne macierze poprzez kwiknięcie na poszczególne komórki macierzy i wpisanie dowolnej wartości całkowitej. Można wprowadzać dane z innych plików ale dane w nich zapisane muszą być zapisane w odpowiednim formacie, który będzie omówiony w dalszej części raportu. Aby tego dokonać w panelu Dane zaznaczamy opcję Z pliku. Program umożliwia tworzenie własnych danych w przypadku wyboru opcji i Własne i wówczas wpisujemy do macierzy własne dane.
Ponadto musimy określić szerokość rzędów hali oraz wybrać algorytm przy pomocy którego zostanie wygenerowane rozwiązanie. Dzięki tej opcji możemy przeprowadzić w łatwy sposób testy zaimplementowanych algorytmów i porównać otrzymane wyniki. Porównanie wyników można przeprowadzić na podstawie wyliczonych kosztów transportu jak i tez czasu obliczeń algorytmów.
Jeżeli wybierzemy algorytm Tabu Search, pojawi się przycisk opisany jako Opcje, wówczas mamy możliwość zmiany parametrów dla tego algorytmu. Możemy wybrać który z algorytmów konstrukcyjnych wykorzystany zostanie do wygenerowania rozwiązania bazowego, które będzie poprawiane przez algorytm TS. Kolejne parametry które możemy zmieniać to:
1. liczba iteracji algorytmu TS dobierana w zależności od rozmiaru zadania (ilości maszyn)
2. maksymalna liczba iteracji po której zostanie zakończony algorytm TS jeżeli nie zostanie znalezione rozwiązanie polepszające funkcje celu. Jest to warunek stopu który można wykorzystać przy minimalizacji kosztów transportu dla zadań o dużych rozmiarach. Dla takich zadań należy ustawić odpowiednio dużą liczbę iteracji algorytmu TS co powoduje, że czas działania programu jest bardzo długi.
3. okres Tabu ( liczba iteracji po której zostaje zdjęty status tabu )
Możliwość zmiany powyższych parametrów czyni program dosyć elastycznym. Na przykład możemy zmieniać liczbę iteracji w zależności od wielkości rozwiązywanego zadania, dzięki czemu możemy ograniczyć czas działania programu.
Po zakończeniu działania algorytmu otrzymujemy rozwiązanie problemu w postaci:
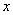 w macierzy Maszyny, oraz dla
każdego rzędu w hali podana jest współrzędna
w macierzy Maszyny, oraz dla
każdego rzędu w hali podana jest współrzędna 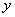 .
.Sposób rozmieszczania maszyn nie jest
przypadkowy, tzn.
maszyny są ustawiane począwszy od pierwszego rzędu od lewej strony
hali,
wskutek czego pierwsza maszyna ma współrzędną 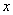 równą połowie jej
szerokości. W następnym rzędzie maszyny są tym razem ustawiane od
prawej strony
hali i tak na przemian. Rząd pierwszy ma współrzędną
równą połowie jej
szerokości. W następnym rzędzie maszyny są tym razem ustawiane od
prawej strony
hali i tak na przemian. Rząd pierwszy ma współrzędną 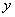 równą 0. Natomiast
współrzędna
równą 0. Natomiast
współrzędna 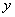 kolejnego rzędu zależy
od najszerszej maszyny przewidzianej do ułożenia w tym rzędzie,
uwzględniając
dodatkowo przestrzeń potrzebną dla wózka przewożącego półprodukty
pomiędzy
maszynami. Współrzędne rzędów są wyświetlane w oknie obrazującym
rozmieszczenie
maszyn na hali, obok prawej ściany hali na wysokości rzędu
kolejnego rzędu zależy
od najszerszej maszyny przewidzianej do ułożenia w tym rzędzie,
uwzględniając
dodatkowo przestrzeń potrzebną dla wózka przewożącego półprodukty
pomiędzy
maszynami. Współrzędne rzędów są wyświetlane w oknie obrazującym
rozmieszczenie
maszyn na hali, obok prawej ściany hali na wysokości rzędu
W przeprowadzonych testach wykorzystano dane przykładowe programu oraz dane pochodzące z innych źródeł, które zostały podane w literaturze w pozycji [3] i [4].
Wszystkie dane testowe muszą być zapisane w plikach tekstowych w formacie opisanym poniżej na rysunku nr 3.
|
17 5 |
liczba wierszy liczba maszyn |
|
78 70 12 60 45 |
szerokości maszyn |
|
0 2 11 9 15 19 0 6 15 8 16 19 0 13 16 2 3 6 0 16 1 11 4 19 0 |
macierz jednostkowych kosztów transportu |
|
0 9 6 2 7 8 0 14 9 11 11 7 0 8 13 1 8 17 0 9 7 12 2 1 0 |
macierz minimalnych odległości między maszynami |
|
0 16 20 19 21 9 0 4 20 23 17 16 0 13 22 6 1 4 0 29 7 23 12 15 0 |
macierz przepływów półproduktów pomiędzy maszynam |
Rys. 3.
Przykładowa
zawartość pliku z zestawem danych
testowych
|
Algorytm |
Konstrukcyjny 1 |
Konstrukcyjny 2 |
Tabu Search |
|||||||
|
Nr Testu |
Ilość Maszyn
|
Szerokość Hali
|
Wartość |
Czas
|
Wartość |
Czas
|
Konstrukcyjny 1 |
Konstrukcyjny 2 |
||
|
Wartość |
Czas
|
Wartość |
Czas
|
|||||||
|
1. |
6 |
200 |
15295 |
21 |
17317 |
22 |
13553 |
295 |
13553 |
293 |
|
2. |
6 |
200 |
7289217,5 |
49 |
8064601,5 |
38 |
4784102,5 |
744037 |
4831000,5 |
744638 |
|
3. |
6 |
300 |
58865 |
7 |
56011 |
6 |
41788 |
361 |
41425 |
404 |
|
4. |
6 |
300 |
36378,5 |
7 |
33286,5 |
6 |
26103,5 |
357 |
32454,5 |
321 |
|
5. |
10 |
200 |
123409,5 |
24 |
134684,5 |
30 |
86646,5 |
2240 |
82054,5 |
3089 |
|
6. |
10 |
200 |
141577 |
9 |
132471 |
7 |
75859 |
3396 |
79791 |
2307 |
|
7. |
10 |
300 |
219539 |
9 |
208970 |
8 |
168375 |
2616 |
168375 |
2563 |
|
8. |
10 |
400 |
234499,5 |
10 |
213339,5 |
8 |
167063,5 |
3797 |
174041,5 |
3198 |
|
9. |
15 |
300 |
538883 |
12 |
482584 |
10 |
298487 |
16775 |
298111 |
15848 |
|
10. |
15 |
300 |
410835 |
15 |
453273 |
12 |
267817 |
17331 |
269347 |
21182 |
|
11. |
15 |
400 |
583073,5 |
15 |
657105,5 |
12 |
448592,5 |
16144 |
470331,5 |
22314 |
|
12. |
15 |
500 |
699300 |
12 |
689657 |
12 |
506046 |
18795 |
499656 |
22728 |
|
13. |
20 |
400 |
1118372 |
21 |
1149066 |
17 |
707624 |
74824 |
707624 |
75426 |
|
14. |
20 |
400 |
1267745,5 |
18 |
1190913,5 |
15 |
651514,5 |
65954 |
676056,5 |
79481 |
|
15. |
20 |
500 |
1801050,5 |
18 |
1832515,5 |
17 |
1266617,5 |
104280 |
1294159,5 |
80150 |
|
16. |
20 |
500 |
1551513 |
20 |
1445474 |
17 |
1049443 |
96039 |
1101802 |
76209 |
|
17. |
25 |
400 |
3241927,5 |
29 |
3367713,5 |
24 |
2241032,5 |
279216 |
2254912,5 |
293593 |
|
18. |
25 |
500 |
3446780 |
31 |
3332692 |
24 |
2410061 |
285439 |
2473501 |
215904 |
|
19. |
25 |
500 |
3674847 |
25 |
3353715 |
21 |
2661829 |
262076 |
2661829 |
262169 |
|
20. |
25 |
600 |
3484455,5 |
24 |
3461217,5 |
21 |
2488217,5 |
184434 |
2413593,5 |
202200 |
|
21. |
30 |
400 |
5855649,5 |
35 |
5832992,5 |
28 |
4244260,5 |
509023 |
3875892,5 |
546562 |
|
22. |
30 |
500 |
5821100,5 |
37 |
6055118,5 |
29 |
3899814,5 |
1513321 |
3899814,5 |
1522199 |
|
23. |
30 |
500 |
5519524,5 |
45 |
6389833,5 |
39 |
3922726,5 |
751283 |
3813438,5 |
754209 |
|
24. |
30 |
600 |
5475884 |
85 |
5726511 |
127 |
4110136 |
1370684 |
4097436 |
1067125 |
|
25. |
30 |
700 |
6048336 |
95 |
6185655 |
86 |
4544273 |
422490 |
4650869 |
514251 |
|
26. |
35 |
600 |
8319732 |
46 |
8021896 |
39 |
5595599 |
1069710 |
5564757 |
1067692 |
|
27. |
35 |
700 |
9527167 |
47 |
9744334 |
45 |
7376829 |
1064627 |
7402006 |
1063418 |
|
28. |
35 |
800 |
9259338,5 |
154 |
9679440,5 |
128 |
7678010,5 |
3486882 |
7678010,5 |
3476422 |
|
29. |
40 |
700 |
12956321 |
181 |
12995810 |
159 |
8807776 |
5934932 |
8910319 |
5938244 |
|
30. |
40 |
800 |
12920174 |
191 |
12756632 |
161 |
9404639 |
5967314 |
9385188 |
5950011 |
|
31. |
40 |
900 |
11550513 |
55 |
12404881 |
43 |
8715440 |
1605850 |
8715440 |
1608438 |
|
32. |
45 |
800 |
18520742,5 |
60 |
19304097,5 |
52 |
12840844,5 |
2570071 |
13212012,5 |
2569433 |
|
33. |
45 |
900 |
16472819,5 |
66 |
18279288,5 |
53 |
12186905,5 |
4450331 |
12134858,5 |
4419310 |
|
34. |
45 |
1000 |
17174757,5 |
111 |
17169962,5 |
92 |
12162140,5 |
4433759 |
12317801,5 |
4440987 |
|
35. |
50 |
700 |
25985008 |
116 |
26184844 |
97 |
18880992 |
5879780 |
18880992 |
5942475 |
|
36. |
50 |
900 |
25214932 |
209 |
22398656 |
176 |
17095565 |
10622436 |
17095565 |
10622219 |
|
37. |
55 |
1000 |
31043240,5 |
82 |
32184260,5 |
69 |
23507327,5 |
5136850 |
23507327,5 |
5144897 |
|
38. |
60 |
1200 |
47651246,5 |
94 |
48569606,5 |
81 |
37712931,5 |
7254608 |
37255507,5 |
7263353 |
|
39. |
70 |
1400 |
66099382,5 |
389 |
70426451,5 |
330 |
49558036,5 |
41612994 |
49558036,5 |
41380412 |
|
40. |
80 |
1500 |
97532201 |
486 |
99909638 |
429 |
75990782 |
305103156 |
75990782 |
305834658 |
Rys. 4.
Tabela
wyników z testów
Przeprowadzono 40 testów dla trzech algorytmów, których wyniki są zamieszczone w tabeli na rysunku nr 4. Dla algorytmu Tabu Search przeprowadzono po dwa testy z tego samego źródła testów z rozróżnieniem na pochodzenie rozwiązania bazowego tj. rozwiązania pochodzącego z algorytmów konstrukcyjnych 1 i 2.
Z przeprowadzonych badań wynika, że algorytm Tabu Search daje rozwiązanie problemu znacznie lepsze niż algorytmy konstrukcyjne. Wśród algorytmów konstrukcyjnych lepszym okazał się algorytm konstrukcyjny 1. Uzyskał lepsze wyniki dla większości testów niż algorytm konstrukcyjny 2. Jednak pod względem czasu wykonywanych obliczeń wyróżnia się algorytm konstrukcyjny 2, ponieważ jest algorytmem o najmniejszej złożoności obliczeniowej. Najwolniej z wszystkich algorytmów działał algorytm Tabu Search, ponieważ jego złożoność obliczeniowa jest dużo większa niż algorytmów konstrukcyjnych.
Testy Dla algorytmu Tabu Search przeprowadzone zostały z następującymi parametrami algorytmu:
· Maksymalna ilość iteracji TS – 30
· Maksymalna ilość iteracji TS bez poprawy funkcji celu – 10
·
Okres tabu 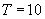
·
Stała różnicowa procesu poszukiwań 
Najlepsze wyniki uzyskano dla algorytmu Tabu Search w którym rozwiązanie bazowe pochodziło od algorytmu konstrukcyjnego 1, który jak się okazało jest najlepszym pod względem otrzymanego rozwiązania algorytmem wśród algorytmów konstrukcyjnych. Czas obliczeń dla Tabu Search w obu przypadkach nie różnił się znacząco tj. uzyskiwano podobne czasy obliczeń.
Algorytm Tabu Search daje rozwiązania dużo lepsze w porównaniu do algorytmów konstrukcyjnych szczególnie wtedy gdy rozmiar zadań tzn. ilość maszyn do rozmieszczenia w hali produkcyjnej jest duża. Ale jest to bardzo czasochłonne, ponieważ złożoność obliczeniowa algorytmu Tabu Search jest wykładnicza, tak jak widać to na rysunku nr 5.
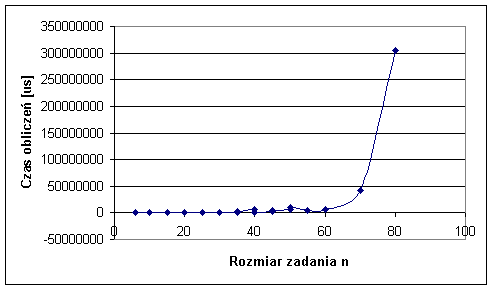
Rys. 5. Czas działania algorytmu Tabu Search w zależności rozmiaru zadania
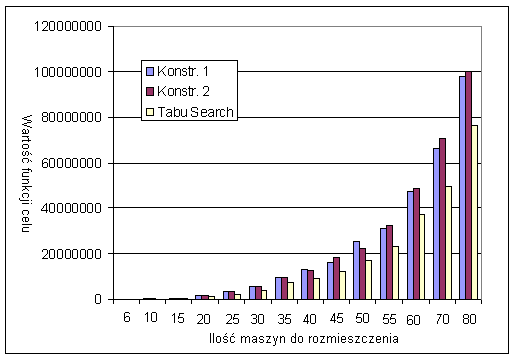
Rys. 6. Wykres otrzymanego rozwiązania z zależności od rozmiaru zadania
Zatem dla mniejszych instancji problemu dobre jest stosować algorytm Tabu Search, natomiast dla dużych instancji tj. dla liczby maszyn przekraczającej 100 maszyn dobrze jest stosować jeden z algorytmów konstrukcyjnych w celu oszczędzenia czasu co również wiąże się z kosztami. Na rysunku nr 6 przedstawiono wykres otrzymanych rozwiązań dla badanych algorytmów w zależności od ilości maszyn do rozmieszczenia w hali. Widać jak algorytm Tabu Search poprawia wartość funkcji celu w stosunku do rozmiaru zadania.
[1] Homel T., Wala K., Metacheurystyka Tabu w optymalizacji wielorzędowego rozmieszczenia maszyn.